Conditional probability

So far, we have seen how probabilities of events are modeled if these events happen without any conditions, e.g. probability of rolling a six, or probability that tomorrow it rains. However, often one has to ask “what if”-questions. E.g., assuming the sun shines tomorrow, what is the probability that the temperature is at least 10 degrees Celsius. Here we want to know the probability of tomorrow's temperature being higher then 10 degrees under the condition that the sun shines.

To answer such questions, we use conditional probability. A conditional probability $\text{Pr}[A|B]$ tells us what the probability of the event $A$ is under the condition that the event $B$ is known to happen or has happened.

For example:

• $\text{Pr}[x+y=12 | x=6]=\frac{1}{6}$ where $x,y$ are independent fair die rolls. Indeed, if you already know that $x=6$, then you just need to know what the probability of $y=6$ is because $x=y=6$ is the only case that leads to $x+y=12$. In contrast, if we do not know what $x$ is, we have $\text{Pr}[x+y=12]=\text{Pr}[x=6]\cdot\text{Pr}[y=6]=\frac{1}{36}$.
• The probability that we have more than 10 degrees Celcius (denoted: $t>10$) tomorrow under the condition that the sun shines (denoted: $w=\text{sun}$) is written $\text{Pr}[t>10|w=\text{sun}]$. We cannot tell what this probability is, but it is likely that $\text{Pr}[t>10|w=\text{sun}] > \text{Pr}[t>10]$. (Meaning, that if the sun shines, the probability of warm weather is higher than on average.)

The formula of conditional probability goes as follows.

Clearly $\text{Pr}[B]>0$ is needed, since in case $\text{Pr}[B]=0$ the formula $\frac{\text{Pr}[A\cap B]}{\text{Pr}[B]}$ is not defined. This means that we cannot ask “what if”-questions that talk about impossible situations. E.g., what is the probability that I can fly if I had wings: $\text{Pr}[\text{"I can fly"}|\text{"I have wings"}]$ is undefined because $\text{Pr}[\text{"I have wings"}]=0$. I just don't have wings, so no probability for the event that I can fly.

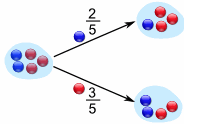
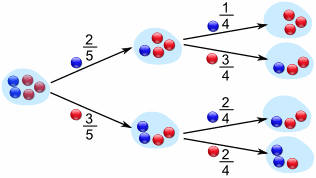
The formula of conditional probability is quite natural. For example, let us view a bag of marbles. Let there be $2$ blue ones and $3$ red ones. One marble is taken out randomly. The probability that a red one was removed is $\frac{2}{5}$ and the probability that a blue one was removed is $\frac{3}{5}$.

Now, if we want to take out a second marble, the probability of obtaining a blue one depends on which color was taken out on first time:

i.e.

$\text{Pr}[\text{"2nd marble is blue"}|\text{"1st marble is blue"}]=\frac{1}{4}$,

$\text{Pr}[\text{"2nd marble is blue"}|\text{"1st marble is red"}]=\frac{2}{4}$.

By multiplying along the branches (in the tree diagram), e.g.,

$\text{Pr}[\text{"1st marble is red"}\cap\text{"2nd marble is blue"}]=\frac{3}{5}\cdot\frac{2}{4}$. That is,

$\text{Pr}[\text{"1st marble is red"}\cap\text{"second marble is blue"}]=$

$\text{Pr}[\text{“1st marble is red”}]\cdot \text{Pr}[\text{“2nd marble is blue”}|\text{“1st marble is blue”}]$

providing the formula of conditional probability $$\frac{\text{Pr}[\text{"1st marble is red"}\cap\text{"second marble is blue"}]}{ \text{Pr}[\text{"1st marble is red"}]}= \text{Pr}[\text{"2nd marble is blue"}|\text{"1st marble is blue"}].$$

Note, that $\Pr[A|B]$ and $\Pr[B|A]$ are quite different things. For example, the probability that a given person will possess more than $100000$ Euro (event $A$) under the condition that he wins the jackpot in the lottery (event $B$) is quite high ($\text{Pr}[A|B]\approx 1$). But the probability that someone wins the lottery jackpot under the condition that he will possess more than $100000$ Euro is not very high (because there are many more likely causes for getting $100000$ Euro than winning in the lottery). Hence, $\text{Pr}[B|A]\approx 0$.

One can, however, in certain cases compute $\text{Pr}[A|B]$ from $\text{Pr}[B|A]$ (and vice versa) using the following theorem:

Sometimes, even if $\text{Pr}[A|B]$ is asked, it is much easier to calculated first $\text{Pr}[B|A]$ (see the exercise below).

Another interesting fact about conditional probabilities is that it gives a new view on independent events. Intuitively, events $A$ and $B$ are independent, if knowing whether $A$ occurs does not tell us whether $B$ occurs. That is, the probability that $B$ occurs should be the same as the probability that $B$ occurs under the condition that $A$ occurs, i.e., mathematically $\Pr[B]=\Pr[B|A]$. This, indeed, is an alternative but equivalent definition of independence as the following result shows: