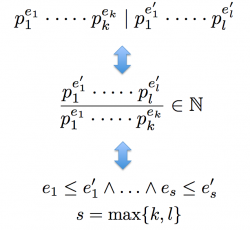Primes and divisibility

A natural number $n$ is a prime number if it has exactly two divisors in $\mathbb N$.

These divisors are $1$, which divides all natural numbers, and the number $n$ itself.

Anyone can easily recall some smallest prime numbers, e.g., $2,3,5,7,11,13,17$ etc. Although in general, determining whether a given (large) number is prime can be a very resource consuming. Also, the location of primes among integers can not be easily computed, however there are many interesting patters, see e.g. Ulam spiral and Prime number theorem.

Show that the set of prima numbers is infinite.

Hint. Start by assuming that the set of prime numbers is finite, for example $\{p_1,\ldots,p_n\}$.

Solution Let us denote with $\mathbb{P}$ the set of prime numbers. Assume the opposite: the set $\mathbb{P}$ is finite and $\mathbb{P}=\{p_1,\ldots,p_n\}$, where $p_1<p_2<\cdots<p_n$. Let $q=p_1p_2\cdots p_n+1$. As $q>p_n$, the number $q$ must have more then two divisors. Moreover, it must be divisible by some prime number — there exists $i$, such that $p_i\mid q$. But we also have $p_i\mid p_1p_2\cdots p_n=q-1$ because this product contains $p_i$. Hence $p_i\mid q-(q-1)=1$ implying that $p_i=1$, which is a contradiction because $1$ is not a prime number.

A natural number is composite if it has more than two divisors.

Note that $1$ is not considered a prime number nor a composite number as it only has one divisor.

In a way, the prime numbers are the ``building blocks'' of all natural numbers (see the following theorem).

Unique factorization theorem. Any natural number $n$ can be represented in exactly one way as a product of prime numbers: $$n = p_1^{e_1} \cdot p_2^{e_2}\cdot \dots \cdot p_k^{e_k} = \prod_{i=1}^k p_i^{e_i},$$ where $p_k$ is the largest prime number that divides $n$ and $e_i \in\mathbb{N}\cup\{ 0\}$ for all $i\in\{1,\dots,k\}$.

Here we denote $p_1 = 2$, $p_2 = 3$, $p_3 = 5$, $p_4 = 7$, $p_5 = 11$, etc. Thus, $p_i$ denote the i-th prime number. For any $i$, the integer $e_i$ is called the index of $n$ at $p_i$.

Some examples of the prime factorization:
$30=2^1 \cdot 3^1 \cdot 5^1$,
$24=2^3 \cdot 3^1$,
$3675=2^0 \cdot 3^1 \cdot 5^2 \cdot 7^2 $.

Note that there can be primes $p_i$ which do not divide $n$ and thus their power $e_i=0$ written to the end of the prime factorisation if needed.

Find the prime factorisations of $4$, $36$, $720$.

Answer $4=2^2$, $36=2^2 \cdot 3^2$, $720=2^4 \cdot 3^3 \cdot 5^1$

The prime factorisations are very tightly related to the divisibility relation.

Given two natural numbers $n$ and $m$ as their prime factorizations $n = p_1^{e_1}\cdot\dots\cdot p_k^{e_k}$ and $m = p_1^{e'_1}\cdot\dots\cdot p_l^{e'_l}$, it is clear that $n \mid m$ if and only if $e_i \leq e'_i$ for all $i \in \{1,\dots,\max\{k,l\}\}$.

For example, $24\not\mid 30$, where
$24=2^{\color{blue}3} \cdot 3^{\color{blue}1}$,
$30=2^{\color{red}1} \cdot 3^{\color{red}1} \cdot 5^{\color{red}1}$,
since for the prime $2$ the required relation between the powers does not hold

primes	$2$	$3$	$5$
relation betveen powers	$\color{blue}3\not\leq \color{red}1$	$\color{blue}1\leq \color{red}1$	$\color{blue}0\leq \color{red}1$

However, $10\mid 30$, where
$10=2^{\color{blue}1} \cdot 3^{\color{blue}0}\cdot 5^{\color{blue}1}$,
$30=2^{\color{red}1} \cdot 3^{\color{red}1} \cdot 5^{\color{red}1}$,
since

primes	$2$	$3$	$5$
relation betveen powers	$\color{blue}1\leq \color{red}1$	$\color{blue}0\leq \color{red}1$	$\color{blue}1\leq \color{red}1$

Use prime factorisation to verify $465 \mid 6975$.

Solution Since $465=2^0\cdot 3^1\cdot 5^1\cdot 7^0\cdot 11^0\cdot 13^0\cdot 17^0\cdot 19^0\cdot 23^0\cdot 29^0\cdot 31^1$ and $6975=2^0\cdot 3^2\cdot 5^2\cdot 7^0\cdot 11^0\cdot 13^0\cdot 17^0\cdot 19^0\cdot 23^0\cdot 29^0\cdot 31^1$. Indeed, $465 \mid 6975$.

This relation between the prime factorisation and divisibility can be used for calculating the greatest common divisor and the least common multiple.

Greatest common divisor and least common multiple