Limit

Let $f$ be a real-valued function defined on some subset of the real line $\mathbb R$. Informally speaking, a number $c$ is said to be the limit of $f$ in the process $x \to \infty$ if $f(x)$ comes arbitrarily close to $c$ as $x$ gets larger and larger. The precise definition of limit is as follows:

Some simple examples:

• $\lim_{x \to \infty} \frac{1}{x} = 0$.
• $\lim_{x \to \infty} 7 = 7$.
• $\lim_{x \to \infty} 7 + \frac{1}{x} - \frac{1}{x^2} = 7$.
• $\lim_{x \to \infty} x = \infty$.
• $\lim_{x \to \infty} -x = -\infty$.
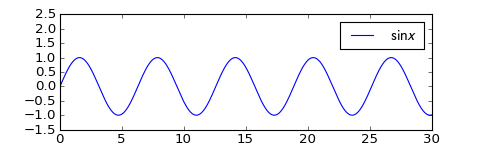
• $\lim_{x \to \infty} \sin x$ does not exist.Explanation This function oscillates between $-1$ and $1$, so it doesn't converge to any number.
  
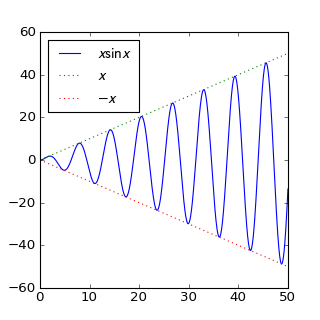
• $\lim_{x \to \infty} x \sin x$ does not exist.Explanation This function oscillates between $-x$ and $x$, so it doesn't have a limit either.
  
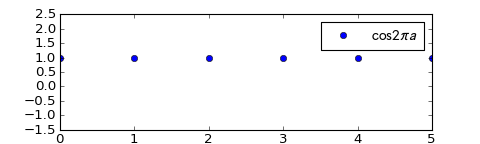
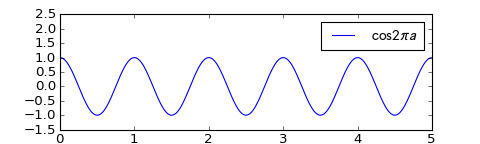
• $\lim_{a \to \infty} \cos(2\pi a) = 1$ if the limit is taken over all natural numbers $a$ but does not exist if the limit is taken over all real numbers $a$.Explanation If we interpret this expression as $\lim_{a \to \infty} f(a)$ where $f : \mathbb N \to \mathbb R,\ a \mapsto \cos(2\pi a)$, then actually $f$ is the constant function $f(a) = 1$, so its limit is $1$.
  
  If we interpret the expression $\lim_{a \to \infty} \cos(2\pi a)$ as $\lim_{a \to \infty} f(a)$ where $f : \mathbb R \to \mathbb R,\ a \mapsto \cos(2\pi a)$ then the limit does not exist, as the function oscillates between $1$ and $-1$ without converging.
  
  So, in such cases, it must be clear from the context whether the limit variable ranges over the reals or only over the integers; often this is reflected by the name of the variable: $n$ almost always denotes an integer and $x$ usually denotes a real number. However, if for a function $f$ the $\lim_{x \to \infty} f(x)$ exists over real numbers $x$, then $\lim_{n \to \infty} f(n)$ also exists over natural numbers $n$ and equals to $\lim_{x \to \infty} f(x)$ over the reals.

If $\lim_{x \to \infty} f(x)$ and $\lim_{x \to \infty} g(x)$ exist and are finite, then

• $\lim_{x \to \infty} f(x) + g(x) = \lim_{x \to \infty} f(x) + \lim_{x \to \infty} g(x)$,
• $\lim_{x \to \infty} f(x) - g(x) = \lim_{x \to \infty} f(x) - \lim_{x \to \infty} g(x)$,
• $\lim_{x \to \infty} f(x) \cdot g(x) = \lim_{x \to \infty} f(x) \cdot \lim_{x \to \infty} g(x)$,
• $\lim_{x \to \infty} \frac{f(x)}{g(x)} = \frac{\lim_{x \to \infty} f(x)}{\lim_{x \to \infty} g(x)}$ if $\lim_{x \to \infty} g(x) \neq 0$.

When one of the limits is infinite, one can use the following rules:

• $q + \infty = \infty$ for $q \neq -\infty$,
• $q - \infty = \infty$ for $q \neq \infty$,
• $q \cdot \infty = \infty$ if $q > 0$,
• $q \cdot \infty = -\infty$ if $q < 0$,
• $q / \infty = 0$ if $q \neq \pm \infty$.

In other cases, like

• $\infty - \infty$,
• $0 \cdot \infty$,
• $q / 0$ where $q \in \mathbb R \cup \{\infty,\, -\infty\}$,

the result is not determined. E. g., knowing that $\lim_{x \to \infty} f(x) = \lim_{x \to \infty} g(x) = \infty$ does not give us any information about whether the limit $\lim_{x \to \infty} f(x) - g(x)$ exists or if it exists then what it is (indeed, for example, $\lim_{x \to \infty} x - x = 0$, $\lim_{x \to \infty} 2x - x = \infty$ and $\lim_{x \to \infty} (x+\sin x) - x$ does not exist at all).

If $\lim_{x \to \infty} g(x) = 0$ then, as said above, knowing only $\lim_{x \to \infty} f(x)$ is not enough to tell what $\lim_{x \to \infty} \frac{f(x)}{g(x)}$ is. However, the situation is better if we also know the signs of $f(x)$ and $g(x)$. For example, $\lim \frac{x}{e^{-x}} = \frac{\infty}{+0} = \infty$, $\lim \frac{x}{-e^{-x}} = \frac{\infty}{-0} = -\infty$. Here $+0$ and $-0$ denote the facts that $\lim_{x \to \infty} e^{-x} = \lim_{x \to \infty} -e^{-x} = 0$ but $e^{-x}$ converges to $0$ from the positive side (i. e. $e^{-x} > 0$) and $-e^{-x}$ converges to $0$ from the negative side.

• $\lim_{x \to \infty} \frac{x^d}{a^{x}} = 0$ for any constants $a > 1, d > 0$.
• $\lim_{x \to \infty} \frac{x^d}{(\log_a x)^b} = \infty$ for any constants $a > 1, b > 0, d > 0$.