For example

A general notation of an $m \times n$ matrix $A$ is

$A=\begin{pmatrix}a_{11} & a_{12} & \dots & a_{1n}\\a_{21} & a_{22} & \dots & a_{2n}\\a_{31} & a_{32} & \dots & a_{3n}\\ \vdots & \vdots & & \vdots\\a_{m1} & a_{m2} & \dots & a_{mn}\end{pmatrix}\hspace{2cm} \text{or}\hspace{2cm} A=(a_{ij}),$

where $i=1,2,\dots , m$ is the row index and $j=1,2,\dots , n$ is the column index. Usually, a capital letter is used for denoting a matrix. Row and column vectors are often denoted by a (noncapital) bold letter, e.g.,

$\mathbf{x}=\begin{pmatrix}x_1 & x_2 & \dots & x_n\end{pmatrix}\hspace{2cm} \text{or}\hspace{2cm} \mathbf{b}=\begin{pmatrix}b_1\\b_2\\\vdots\\b_m\end{pmatrix}.$

Matrices can be added, multiplied by a scalar, and multiplied by other matrices. Formulas for the operations are as follows

The diagram to the right describes also matrix multiplication.

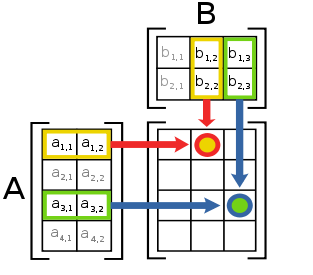
Here are multiplied matrices $A$ with dimension $4\times 2$ and $B$ with dimension $2\times 3$. The matrix $AB$ is with dimension $4\times 3$.

Let $AB=(c_{ij})$. Then

$c_{12}=a_{11}b_{12}+a_{12}b_{22}$

and

$c_{33}=a_{31}b_{13}+a_{32}b_{23}$.

from numpy import array
 
M1 = array([[0,3,1],[3,-1,7],[-5,14,-8],[7,2,9],[0,-6,10]]) # the first matrix
M2 = array([[6],[1],[-1]])                                  # the second matrix
R = numpy.zeros(shape=(len(M1),len(M2.T)))                  # the result matrix filled with zeros
 
for i in range(len(M1)):                                    # loop over rows of M1; row i in matrix M1 is 
    R[i]=sum(M1[i,:]*M2[:,0])                               # multiplied elementwise with column 0 from M2,
                                                            # elements in the product are added
print R

from numpy import array
 
M1 = array([[2,10,7],[1,4,3]])               # the first matrix
M2 = array([[1,6,4],[2,3,1],[2,1,10]])       # the second matrix
R = numpy.zeros(shape=(len(M1),len(M2.T)))   # the product filled with zeros
 
for i in range(len(M1)):
    for  j in range(len(M2.T)):
        R[i,j]=sum(M1[i,:]*M2[:,j])          # M1 row i multiplied elementwise with M2 column j and summed
 
print R%3                                    #for every element in R the residue modulo 3 is calculated

Another important operation on matrices is that of taking the transpose. It is denoted by placing a $T$ as an exponent on the initial matrix.

Thus taking the transpose means reorganize matrix entries so that row of the initial matrix will be columns in the transpose. First row will be first column, second row will be second column and so on.

from numpy import array
 
M1 = array([[1,5],[4,3],[5,4]])          # the first matrix
M2 = array([[1],[2],[3]])                # the second matrix
M3 = array([[1],[2],[3]])                # the third matrix
R = numpy.zeros(shape=(len(M1),len(M1))) # the product matrix filled with zeros
 
for i in range(len(M1)):
    for  j in range(len(M1)):
        R[i,j]=sum(M1[i,:]*M1.T[:,j])    # M1 row i multiplied elementwise with M1 transp. column j, summed
 
print 5*R+M2*M3.T

Sum of matrices, scalar multiplication, matrix multiplication and the transpose are basic matrix operations. These operations have several useful properties. For example, knowing that $$c\cdot A+c\cdot B=c\cdot (A+B),$$ where $A$ and $B$ are matrices and $c$ is a constant, it is possible to reduce number of multiplications. Thus, instead of

$$-2\cdot\begin{pmatrix}10 & -3\\-8 & 5\\20 & 3\end{pmatrix}\!+\!(-2)\cdot\begin{pmatrix}-8 & 4\\6 & 3\\-15 & 17\end{pmatrix}=\begin{pmatrix}-2\color{red}\cdot10 & -2\color{red}\cdot(-3)\\-2\color{red}\cdot(-8) & -2\color{red}\cdot5\\-2\color{red}\cdot20 & -2\color{red}\cdot3\end{pmatrix}\!+\!\begin{pmatrix}-2\color{red}\cdot(-8) & -2\color{red}\cdot4\\-2\color{red}\cdot6 & -2\color{red}\cdot3\\-2\color{red}\cdot(-15) & -2\color{red}\cdot17\end{pmatrix}\!=\!\begin{pmatrix}-4 & -2\\4 & -16\\-10 & -40\end{pmatrix},$$ which is $12$ multiplications, we can manage only with $6$:

$$-2\cdot\!\begin{pmatrix}10 & -3\\-8 & 5\\20 & 3\end{pmatrix}\!+\!(-2)\cdot\!\begin{pmatrix}-8 & 4\\6 & 3\\-15 & 17\end{pmatrix}=-2\cdot\!\Bigg[\begin{pmatrix}10 & -3\\-8 & 5\\20 & 3\end{pmatrix}\!+\!\begin{pmatrix}-8 & 4\\6 & 3\\-15 & 17\end{pmatrix}\Bigg]=-2\cdot\!\begin{pmatrix}2 & 1\\-2 & 8\\5 & 20\end{pmatrix}\!=\!\begin{pmatrix}-4 & -2\\4 & -16\\-10 & -40\end{pmatrix}.$$

Let $A$, $B$ and $C$ be matrices such that all the operations below are defined, and let $k$ and $l$ denote some constants (for example real numbers) . Here are some additional useful properties concerning the matrix operations: